08. Mandelbrot Set - The Art of Complex Numbers
Today, we will try to tackle a simple but intricate concept called
the Mandelbrot Set. The Mandelbrot set is the set of complex numbers C for which the function Fc(z) = z^2 + c does not diverge to infinity when iterated from z = 0, i.e., for which the sequence Fc( 0 ), Fc ( Fc ( 0 ) ),
etc., remains bounded in absolute value. The resulting visual pattern
is intricate and will remain unchanged even when you zoom in. This was
first defined and drawn by Robert W. Brooks and Peter Matelski in 1978.
It may look too complicated at first, but it is in fact quite simple
if you consider the real and imaginary values separately as a and b.
z = a + bi
We will start with the equation
Fc(z) = z^2 + c
Here c is a complex number and the idea is to start with z = 0
and iterate the equation over and over by feeding the new z back into
the equation. In theory, this should bring the result to a certain value
instead of moving on to infinity. However, in the real world, we can't
iterate this forever; therefore we will stop after a certain number of
iterations. To implement this mathematically, we must know how to
multiply two complex numbers. This is well explained in this article. With this, we can see that the result of z^2 is:
z^2 = a^2 + 2abi - b^2
In order to implement this in code, we must perform this calculation on each of the pixels on the screen; and yes, it will take some time for the computer to do it. However, we must not work with the exact values of the width and height of the screen. Doing this will result in a tiny image on the screen. Therefore we must map the width and height of the screen between two values that can create a visible Mandelbrot set. So we will define two global variables that store this range as well as how many iterations we must perform.
int maxIter = 100;
float[] range = {-1.5, 1.5};
Next, we will consider each of these pairs of numbers as the real and imaginary parts of the constant c and perform the equation. Doing this is easy and will result in the code below.
// C is the constant we consider in each iteration
float ca = map(x, 0, height, range[0], range[1]); // Real component of C
float cb = map(y, 0, height, range[0], range[1]); // Imaginary component of C
// We define a variable n to know how many iterations deep we've gone
float n = 0;
// In the first iteration, as initial z = 0, z1 = c
float a = ca; // Real component of z
float b = cb; // Imaginary component of z
// Now we calculate z over and over again until we reach a
// certain maximum iterations
while (n < maxIter) {
// We calculate zi = zi-1 = zi^2 + c
float aa = a * a - b * b; // Real part of zi^2
float bb = 2 * a * b; // Imaginary part of zi^2
// Adding the c constant to z^2
a = aa + ca; // New real part of z
b = bb + cb; // New imaginary part of z
// If the value of z tends towards infinity, we stop
if (abs(aa + bb) > 64) {
break;
}
n++;
}
What's left is to map the resulting number of
iterations as the colour at that point on the canvas. This is done by
first converting the colour mode at setup to colorMode(HSB)
and then applying it to a circle at that point. We will also smooth
this value for better colour variation. Since we consider the case of
infinity as zero, we change its brightness to 0 as well.
float bright = map(n, 0, maxIter, 0, 1);
bright = map(sqrt(bright), 0, 1, 0, 255);
if (n == maxIter) {
bright = 0;
}
fill(bright, 255, bright * 1.5);
circle(x, y, 10);
The end result will be something as shown below.

With this, we can conclude the Mandelbrot set.
Julia Set
There also exists an alternative to Mandelbrot Set derived from itself called the Julia Set. Julia Set is similar to Mandelbrot Set but instead of adding C in a loop, we first start with z = z^2 + C where C is a range of complex numbers as usual and in the next iteration we switch to z = z^2 + C' where C' is a constant pre-made. With different values to C', we get much more elaborate designs.
Julia Set can be achieved by replacing the below code part with the code part given after that.
a = aa + ca; // New real part of z
b = bb + cb; // New imaginary part of z
a = aa + C[0]; // New real part of z
b = bb + C[1]; // New imaginary part of z
We must also define C to be float[] C = {0.37, 0.1} as a global variable. This will hold the Julia Set constants.
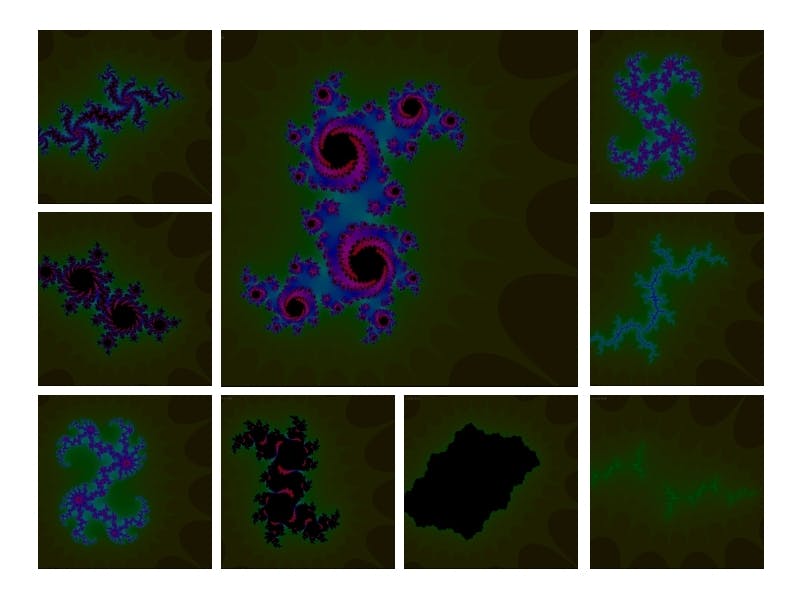
To have a better view of each render, in the Github repository switch to the main branch and look in the output folder.
External Links:
- Github Repository with the Processing Code: Github Repository
- Wikipedia article on Mandelbrot Set: wikipedia.org
- Wikipedia article on Julia Set: wikipedia.org
- Julia Set Fractal site by Paul Bourke: paulbourke.net
- The Coding Train video on Mandelbrot Set: youtube.com
- The Coding Train video on Julia Set: youtube.com


Comments
Post a Comment